Blog

数据结构 - 树

Posted by Kylin Soong on Oct 27, 2016 categorized as java

基本概念

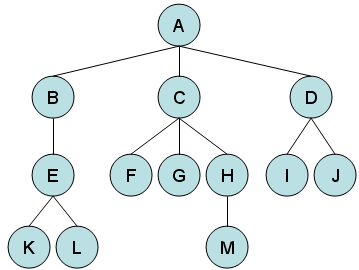
Tree Overview

  • 根(root)
  • 边(edge)
  • 儿子(child)
  • 父亲(parent)
  • 一棵树有 N 个节点和 N - 1 条边
  • 兄弟(siblings)
  • 祖父(grandparent)
  • 孙子(grandson)
  • 路径(path) - 树中任意两个节点之间只有一条路径
  • 深度(depth) - 树中任意两个节点之间路径的长度
  • 高(height) - 树中最长的路径
  • 祖先(ancestor)
  • 后裔(decendant)
  • 真祖先(proper ancestor)
  • 真后裔(proper decendant)

树的实现

public class TreeNode<T> {
    T element;
    TreeNode<T> firstChild;
    TreeNode<T> nextSibling;
}

树的两种遍历方式

  1. 前序遍历(preorder traversal) - 对节点的处理在它的诸儿子节点被处理之前进行
  2. 后序遍历(postorder traversal) - 对节点的处理在它的诸儿子节点被处理之后进行

二叉树

二叉树(binary tree) 是特殊的树 - 树中的每个节点都不能有多于两个的儿子.

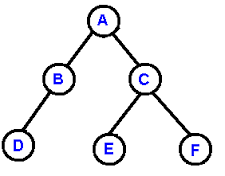
Tree binary tree

二叉树的实现

public class BinaryNode<T> {
    T element;
    BinaryNode<T> left;
    BinaryNode<T> right;
}

二叉树的三种遍历方式

  1. 前序遍历(preorder traversal) - 对节点的处理在它的诸儿子节点被处理之前进行
  2. 中序遍历(inorder traversal) - 处理节点之前先处理左节点，处理节点之后再处理后节点
  3. 后序遍历(postorder traversal) - 对节点的处理在它的诸儿子节点被处理之后进行

查找树 ADT - 二叉查找树

定义

  • 树中每个节点 X，它的左子树中所有的节点对应的值小于节点 X 的值.
  • 二叉查找树的平均深度是 O(log N)
  • 二叉查找树要求所有节点都能够排序

二叉查找树的实现

public class BinarySearchTree<T extends Comparable<? super T>> {

    private BinaryNode<T> root;
    
    public BinarySearchTree() {
        this.root = null;
    }
    
    public void makeEmpty() {
        this.root = null;
    }
    
    public boolean isEmpty() {
        return this.root == null ;
    }
    
    public boolean contains(T x) {
        return contains(x, root);
    }
    
    public T findMin() {
        if(isEmpty())
            throw new UnderflowException();
        return findMin(root).element;
    }

    public T findMax() {
        if(isEmpty())
            throw new UnderflowException();
        return findMax(root).element;
    }
    
    public void insert(T x) {
        this.root = insert(x, root);
    }

    public void remove(T x) {
        this.root = remove(x, root);
    }
    
    public void printTree() {
        printTree(root);
    }
}
contains 方法
    private boolean contains(T x, BinaryNode<T> t) {
        
        if(null == t)
            return false;
        
        int compareResult = x.compareTo(t.element);
        if(compareResult < 0) {
            return contains(x, t.left);
        } else if(compareResult > 0) {
            return contains(x, t.right);
        } else {
            return true;
        }
    }
findMin 方法
    private BinaryNode<T> findMin(BinaryNode<T> t) {
        
        if(t == null) {
            return null;
        } else if (t.left == null) {
            return t;
        }
        
        return findMin(t.left);
    }
findMax 方法
    private BinaryNode<T> findMax(BinaryNode<T> t) {
        
        if(t == null) {
            return null;
        } else if(t.right == null) {
            return t;
        }
        
        return findMax(t.right);
    }
insert 方法
    private BinaryNode<T> insert(T x, BinaryNode<T> t) {
        
        if(null == t)
            return new BinaryNode<>(x, null, null);
        
        int compareResult = x.compareTo(t.element);
        if(compareResult < 0) {
            t.left = insert(x, t.left);
        } else if(compareResult > 0) {
            t.right = insert(x, t.right);
        }

        return t;
    }
remove 方法
    private BinaryNode<T> remove(T x, BinaryNode<T> t) {
        
        if(null == t)
            return t;
        
        int compareResult = x.compareTo(t.element);
        if(compareResult < 0) {
            t.left = remove(x, t.left);
        } else if (compareResult > 0) {
            t.right = remove(x, t.right);
        } else if(t.left != null && t.right != null) {
            t.element = findMin(t.right).element;
            t.right = remove(t.element, t.right);
        } else {
            t = (t.left != null) ? t.left : t.right;
        }
        
        return t;
    }
printTree 方法
    private void printTree(BinaryNode<T> t) {
        if(t != null) {
            printTree(t.left);
            System.out.println(t.element);
            printTree(t.right);
        }
    }

示例

1. 通过 insert 初始化树

本示例通过 insert 初始化树的形状如下

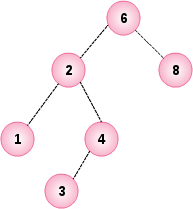
Binary Search Tree Example 1

后面示例中不做特别说明都使用本示例中如上所示的树。

BinarySearchTree<Integer> tree = new BinarySearchTree<Integer>();
tree.insert(6);
tree.insert(2);
tree.insert(1);
tree.insert(4);
tree.insert(3);
tree.insert(8);
2. 添加新节点

如下图所示，我们向示例 1 中的树添加新节点 5

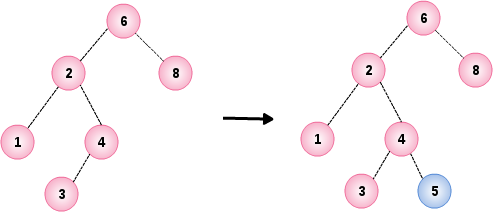
Binary Search Tree Example 2

BinarySearchTree<Integer> tree = sample1();
tree.insert(5);
3. 查找最大和最小节点

基于示例 1 中的树通过如下代码查找最大和最小节点

BinarySearchTree<Integer> tree = sample1();
System.out.println(tree.findMax());
System.out.println(tree.findMin());

运行结果输出

8
1
4. 查找树中是否包含某节点

基于示例 1 中的树通过如下代码查找树中是否包含某节点

BinarySearchTree<Integer> tree = sample1();
System.out.println(tree.contains(8));
System.out.println(tree.contains(5));

运行结果输出

true
false
5. 删除只有一个子节点的节点

基于示例 1 中的树的节点 4 只有一个左节点3，本示例演示删除节点4，结果如下图

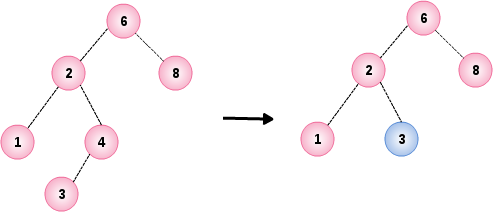
Binary Search Tree Example 3

BinarySearchTree<Integer> tree = sample1();
tree.remove(4);
6. 删除有两个子节点的节点

基于示例 1 中的树的节点 2 只有一个左节点 1 和一个右节点 4，本示例演示删除节点 2，结果如下图

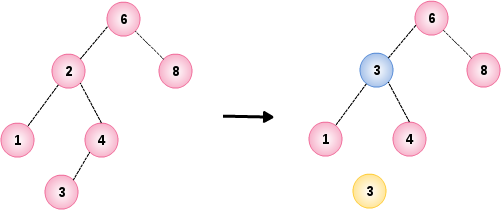
Binary Search Tree Example 4

BinarySearchTree<Integer> tree = sample1();
tree.remove(2);

NOTE: 删除有两个子节点的节点的策略是用该节点右子树中最小的节点替换该节点

7. 发生多次替换的复杂节点删除

如下左图，删除树中节点 2，节点 2 右子树中最小的节点为 3，且 节点 3 有右子树

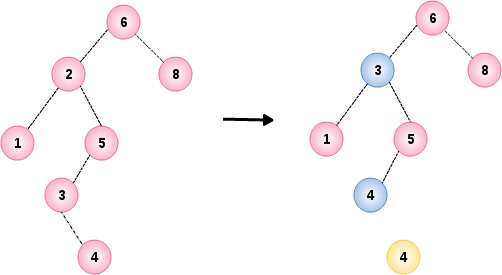
Binary Search Tree Example 5

BinarySearchTree<Integer> tree = sample2();
tree.remove(2);

NOTE: 如上删除过程发生了两次节点替换：节点 2 替换 节点 2 右子树最小的节点 3；节点 3 替换 节点 3 右子树最小的节点 4.

AVL 树 - 带有平衡条件的二叉查找树(Self-balancing binary search tree)

定义

  • AVL 树是带有平衡条件的二叉查找树(Self-balancing binary search tree)
  • 平衡条件指树中每个节点都有相同高度的左子树和右子树
  • 理想平衡树(perfectly lalanced tree) 指由 2^k -1 个节点组成，每个节点都有一个左儿子和右儿子
  • AVL 树是其每个节点的左子树和右子树的高度最多差 1 的二叉查找树
  • AVL 树高度一般略大于 log N，时间复杂度约为 O(log N)
  • 对 AVL 树的插入可能破坏树的平衡条件，通过旋转(rotation)来修正

AVL 树的两种旋转方式

对 AVL 树的插入可能破坏树的平衡条件，通过旋转(rotation)来修正，AVL 树有两种旋转方式:

  • 单旋转(single rotation) - 插入发生在”外边”(左儿子的左子树或右儿子的右子树)破坏树的平衡条件，通过单旋转调整
  • 双旋转(double rotation) - 插入发生在”内部”(左儿子的右子树或右儿子的左子树)破坏树的平衡条件，通过双旋转调整

AVL 树的实现

  • AVLNode
public class AVLNode<T> {
    T element;
    AVLNode<T> left;
    AVLNode<T> right;
    int height;
}
  • AVLTree
public class AVLTree<T extends Comparable<? super T>> {
    
    private static final int ALLOWED_IMBALANCE = 1;
    
    private AVLNode<T> root;
    
    public AVLTree() {
        this.root = null;
    }
    
    public void makeEmpty() {
        this.root = null;
    }
    
    public boolean isEmpty() {
        return this.root == null;
    }
    
    public void insert(T x) {
        this.root = insert(x, root);
    }
    
    public void remove(T x) {
        this.root = remove(x, root);
    }
    
    public T findMin() {
        if(isEmpty())
            throw new UnderflowException();
        return findMin(root).element;
    }
    
    public T findMax() {
        if(isEmpty())
            throw new UnderflowException();
        return findMax(root).element;
    }
    
    public boolean contains(T x) {
        return contains(x, root);
    }
    
    public void printTree() {
        if(isEmpty())
            System.out.println("Empty tree");
        else
            printTree(root);
    }
}

比较二叉查找树的实现 和 AVL 树的实现比较

  • contains, findMin, findMax, printTree 方法的实现相同
  • insert, remove AVL 树的实现较二叉查找树的实现复杂，插入和删除后需要考虑树的平衡条件, 通过一个 balance 方法实现
  • AVL 树的节点有深度属性，通过 height 方法来计算节点的深度
contains 方法
    private boolean contains(T x, AVLNode<T> t) {
        
        if(t == null)
            return false;
        
        int compareResult = x.compareTo(t.element);
        if(compareResult < 0) {
            return contains(x, t.left);
        } else if(compareResult > 0) {
            return contains(x, t.right);
        } else {
            return true;
        }
    }
findMin 方法
    private AVLNode<T> findMin(AVLNode<T> t) {
        
        if(t == null){
            return null;
        } else if(t.left == null){
            return t;
        }
        return findMin(t.left);
    }
findMax 方法
    private AVLNode<T> findMax(AVLNode<T> t) {
        
        if(t == null) {
            return null ;
        } else if(t.right == null) {
            return t;
        }
        return findMax(t.right);
    }
height 方法
    private int height(AVLNode<T> t) {
        return t == null ? -1 : t.height;
    }
balance 方法
    private AVLNode<T> balance(AVLNode<T> t) {
        
        if (t == null)
            return t;
        
        if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) {
            if (height(t.left.left) >= height(t.left.right)) {
                t = rotateWithLeftChild(t);
            } else {
                t = doubleWithLeftChild(t);
            }
        } else if(height(t.right) - height(t.left) > ALLOWED_IMBALANCE) {
            if (height(t.right.right) >= height(t.right.left)) {
                t = rotateWithRightChild(t);
            } else {
                t = doubleWithRightChild(t);
            }
        } 
        
        t.height = Math.max(height(t.left), height(t.right)) + 1 ;
        return t;
    }
rotateWithLeftChild, doubleWithLeftChild, rotateWithRightChild, doubleWithRightChild 方法
    private AVLNode<T> rotateWithLeftChild(AVLNode<T> k2) {
        AVLNode<T> k1 = k2.left;
        k2.left = k1.right;
        k1.right = k2;
        k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ;
        k1.height = Math.max(height(k1.left), k2.height) + 1;
        return k1;
    }

    private AVLNode<T> rotateWithRightChild(AVLNode<T> k1) {
        AVLNode<T> k2 = k1.right;
        k1.right = k2.left;
        k2.left = k1;
        k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
        k2.height = Math.max(height(k2.right), k1.height) + 1;
        return k2;
    }

    private AVLNode<T> doubleWithLeftChild(AVLNode<T> k3) {
        k3.left = rotateWithRightChild(k3.left);
        return rotateWithLeftChild(k3);
    }

    private AVLNode<T> doubleWithRightChild(AVLNode<T> k1) {
        k1.right = rotateWithLeftChild(k1.right);
        return rotateWithRightChild(k1);
    }
insert 方法
    private AVLNode<T> insert(T x, AVLNode<T> t) {
        
        if( t == null) 
            return new AVLNode<>(x, null, null);
        
        int compareResult = x.compareTo(t.element);
        if(compareResult < 0) {
            t.left = insert(x, t.left);
        } else if(compareResult > 0) {
            t.right = insert(x, t.right);
        }
        
        return balance(t);
    }
remove 方法
    private AVLNode<T> remove(T x, AVLNode<T> t) {
        
        if(t == null)
            return t;
        
        int compareResult = x.compareTo(t.element);
        if(compareResult < 0) {
            t.left = remove(x, t.left);
        } else if(compareResult > 0) {
            t.right = remove(x, t.right);
        } else if(t.left != null && t.right != null) {
            t.element = this.findMin(t.right).element;
            t.right = remove(t.element, t.right);
        } else {
            t = (t.left != null) ? t.left : t.right;
        }
        
        return balance(t);
    }
printTree 方法
    private void printTree(AVLNode<T> t) {

        if(t != null) {
            printTree(t.left);
            System.out.println(t.element);
            printTree(t.right);
        }
    }

示例

本示例从初始化的空 AVL 树开始插入节点 3，2，1，4 ~ 7，倒序插入节点 10 ~ 16，接着在插入节点 8 和节点 9. 本示例的目的是演示 AVL 树如何通过旋转保持平衡条件。

01. 插入节点 3，2，1
AVLTree<Integer> tree = new AVLTree<>();
tree.insert(3);
tree.insert(2);
tree.insert(1);

在插入节点 1 时 AVL 树的平衡条件在根节点3 处被破坏，通过根节点 3 和它的左儿子 2 之间实行单旋转进行修正:

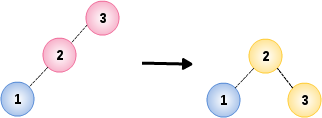
AVL Tree Example 1

02. 插入节点 4，5
tree.insert(4);
tree.insert(5);

插入节点 4 没有问题，但在插入节点 5 时破坏了节点 3 的平衡条件，通过节点 3 和它的右儿子 4 之间实行单旋转进行修正

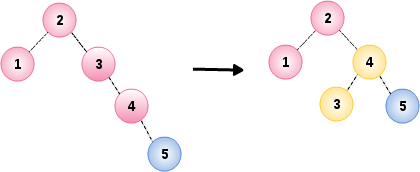
AVL Tree Example 2

03. 插入节点 6
tree.insert(6);

插入节点 6 导致根节点 2 的平衡条件破坏，通过节点 2 和它的右儿子 4 之间实行单旋转进行修正

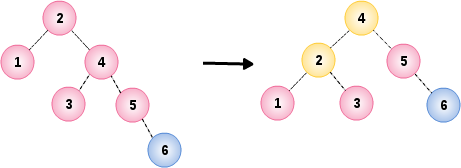
AVL Tree Example 3

04. 插入节点 7
tree.insert(7);

插入节点 7 时破坏了节点 5 的平衡条件，通过节点 5 和它的右儿子 6 之间实行单旋转进行修正

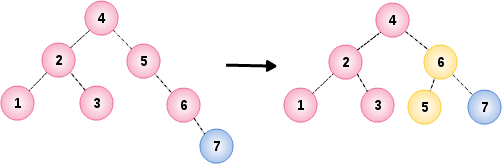
AVL Tree Example 4

05. 插入节点 16，15
tree.insert(16);
tree.insert(15);

插入节点 16 没有问题，但在插入节点 15 时破坏了节点 7 的平衡条件，通过节点 7，16 和 15 的双旋转修正

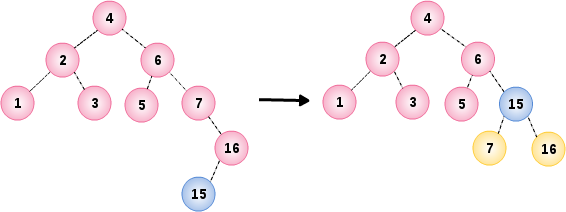
AVL Tree Example 5

06. 插入节点 14
tree.insert(14);

插入节点 14 时破坏了节点 6 的平衡条件，通过节点 6，15 和 7 的双旋转修正

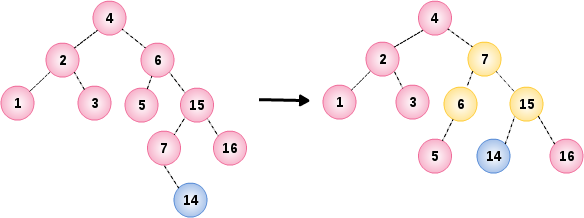
AVL Tree Example 6

07. 插入节点 13
tree.insert(13);

插入节点 13 导致根节点 4 的平衡条件破坏，通过节点 4 和它的右儿子 7 之间实行单旋转进行修正

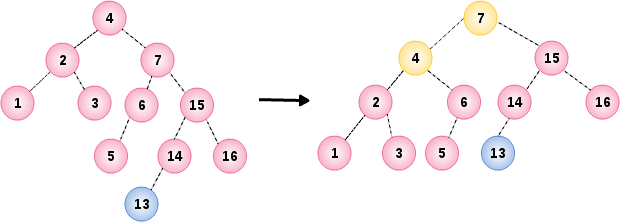
AVL Tree Example 7

08. 插入节点 12
tree.insert(12);

插入节点 12 导致根节点 14 的平衡条件破坏，通过节点 14 和它的左儿子 13 之间实行单旋转进行修正

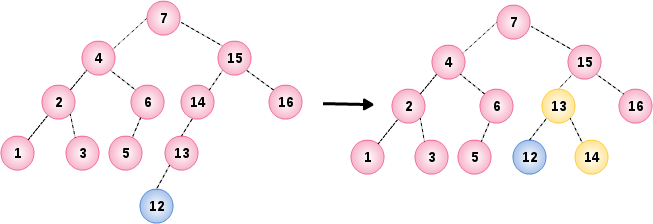
AVL Tree Example 8

09. 插入节点 11
tree.insert(11);

插入节点 11 导致根节点 15 的平衡条件破坏，通过节点 15 和它的左儿子 13 之间实行单旋转进行修正

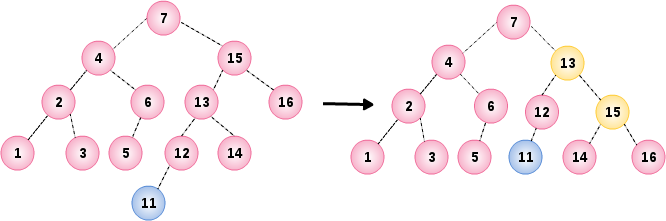
AVL Tree Example 9

10. 插入节点 10
tree.insert(10);

插入节点 10 导致根节点 12 的平衡条件破坏，通过节点 12 和它的左儿子 11 之间实行单旋转进行修正

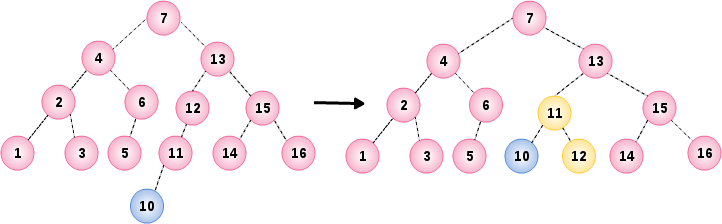
AVL Tree Example 10

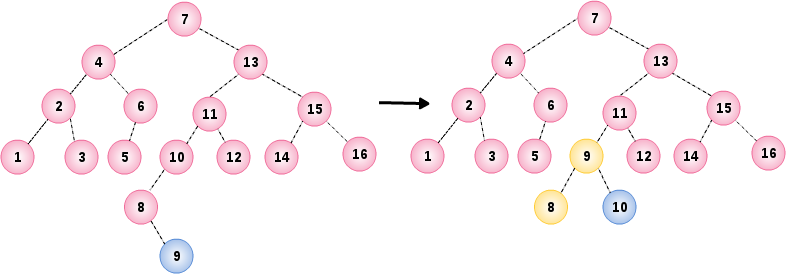
11. 插入节点 8，9
tree.insert(8);
tree.insert(9);

插入节点 8 没有问题，但在插入节点 9 时破坏了节点 10 的平衡条件，通过 9，10 和 8 之间进行一个双旋转调整

AVL Tree Example 11

B 树

定义

B 树属二叉查找树数据模型的范畴，而且具有带有平衡条件的二叉查找树的特点，阶为 M 的 B 树具有一下特征:

  1. 数据项存储在树叶上
  2. 非叶子节点存储直到 M - 1 个关键字以指示搜索的方向；关键字 i 代表子树 i + 1 中的最小的关键字
  3. 树的根或者是一片树叶，或者其儿子数在 2 和 M 之间
  4. 除根外，所有非树叶节点的儿子在 M/2 和 M 之间
  5. 所有的树叶都在相同的深度上并有 L/2 和 L 之间个数据项